りんぼくです。
線状探索法に関する過去問で苦しんだので、誰でも解けるように解説を放流します。
解き方を考えるにあたっての参考書
基本情報技術者試験の線状探索過去問の解き方
1,2,3,4,5,6,7,8,9,10,11
のように並んだデータ構造があるとして、頭から総当たりで検索していくのが線状探索法。
1回目で目的のデータが見つかることもあれば、11回目で見つかることもあります。
平均参照回数を求める問題が出ます。
最遅と最速の平均を取ると求められます。
11 + 1 / 2 = 6
データが大量の場合は、+1 を無視する場合もあります。
参照回数の計算式 x + 1 / 2
x個並んだデータからデータを見つける時、最速が1回、最遅がn回だからその平均を取ると
x回+1回 / 2(平均を取る対象が最速と最遅の2つの値だから2)
過去問の解き方を放流します
異なるn個のデータが昇順に整列された表がある。この表をm個のデータごとのブロックに分割し,各ブロックの最後尾のデータだけを線形探索することによって,目的のデータの存在するブロックを探し出す。次に,当該ブロック内を線形探索して目的のデータを探し出す。このときの平均比較回数を表す式はどれか。ここで,mは十分大きく,nはmの倍数とし,目的のデータは必ず表の中に存在するものとする。
午前免除試験 R4-1月 問9 より
この問題は、平均参照数を2回求める必要があります。
選択肢は
ア m + n /m
イ m/2 + n/2m
ウ n/m
エ n /2m
平均参照数1回目
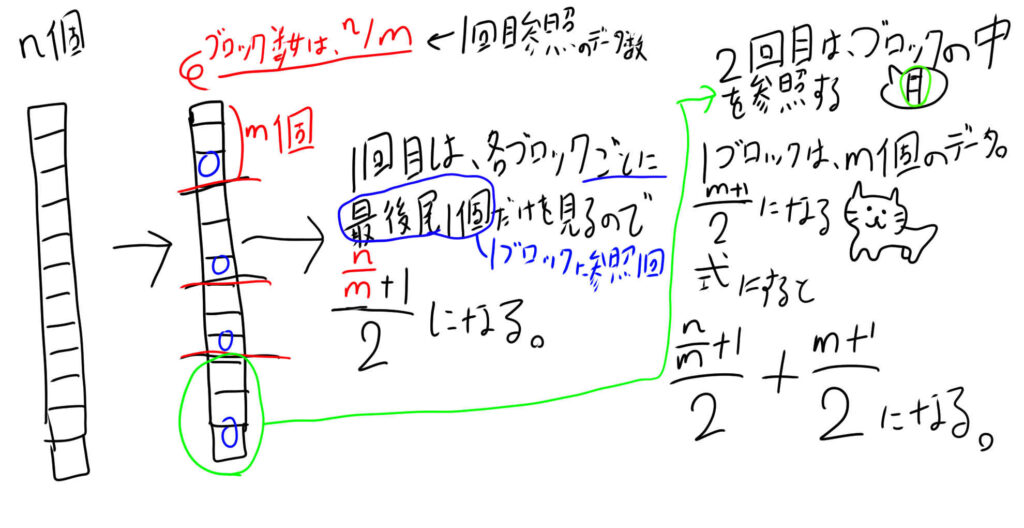
この表をm個のデータごとのブロックに分割し,各ブロックの最後尾のデータだけを線形探索することによって,目的のデータの存在するブロックを探し出す。
- 全体として、n個のデータがあるデータ構造がある。(ソートされてる)
- ソートされており、ブロック1個につき参照は1回。(ソートされていて、ブロックの最後尾だけを見るから)
- n個のデータを複数個のブロックに分割している(ブロックの個数は?)
- それぞれのブロックにはm個ずつデータが入っている(つまりブロックの個数はn/m)
- まずは、「n/m個からなるデータを線状探索した場合の平均参照数を求める」
- 平均参照数を求める公式に当てはめると ((n/m) + 1 )/2 となる。
平均参照数2回目
次に,当該ブロック内を線形探索して目的のデータを探し出す。
- 1ブロックには、m個のデータが入っている
- 1回目の参照で、参照するべきブロックが1個に絞られている
- 平均参照回数を求める公式に当てはめると(m + 1) / 2となる。
このときの平均比較回数を表す式 = 参照1回目+参照2回目
(((n/m) + 1 )/2) + ((m + 1) / 2)
式を整える
問題文に「十分に大きい」とあるので、最終的には+1を無視して答えを探します。
解いてる途中は無視してません。

よって正解の選択肢は
イ m/2 + n/2m



コメント