進数変換についてミリ知らな私がつまづきまくったポイントを、メモします。
基本情報で最初の3ページを攻略して先に進むための記事です!
私は算数の学習をかなり早い段階、まさに数学ではなく算数の段階で挫折しているため、
変数の変換問題の解き方については、まさに「ミリ知ら」からのスタートです。
計算をする前に「基数」と「重み」という概念を知っていきましょう。
この記事では少数や分数や負の数は扱いません。
テキストで勉強する時、最初の1ページを攻略するための記事です。
そもそも2進数や16進数、8進数をやる意味があるのか?
なくはないと思いますが、「基本情報技術者試験の計算問題」は私は大嫌いで、できる限りわかりやすい解説をしてその足ぎりを意味のないことにすることが私の目標です。
話が通じない人の答えみたいになっちゃいますが、
IT系の就職である程度指標とされる「基本情報技術者試験」の問題に含まれているから、やる意味があると思ってます。
あとは、よりコンピュータに寄り添った言語で開発するときには、10進数は通じなかったりします。
環境によって、やる意味があるかないかの感じ方は違ってくると思います。
エンジニアとしてコンピュータを扱っている以上、どこかで別の10進数以外をみることにはなるので
「F8...? なんだこの文字列は...?」
ではなく、
「F8...248か。あれ、あそこで定義した定数と同じだな。」
とパッとわかる方が、事象の把握に役立つことは確かです。
2進数はON(1)とOFF(0)だけのコンピュータが扱う数値
電気信号で動くコンピュータは、電気と同じでONとOFF、1と0で全てを表現します。
あとは、バイナリデータを弄って遊んだことがある人はわかると思いますが、人間が見える範囲では16進数も使われていたりします。
そのためか、基本情報技術者試験では2進数をはじめとした8進数、16進数の計算問題が出るそうです。
基本情報の進数変換で出てくる「基数」とは何なのか?
基本情報技術や試験の進数変換で私にとっての一番最初のつまずきポイントは「基数」という言葉への理解でした。
大前提として、「基数は、私たちが扱う10進数にとって都合が良いものであり、他の進数と10進数として扱うために使う便利ツール」です。
2進数の基数は2、8進数の基数は8、16進数の基数は16です。
10進数にとって都合が良い基数を使うことで、2進数>10進数変換、10進数>2進数変換を計算できるようになります。
他の進数についても同じため、16進数から2進数への計算が必要になったときに、16進数>10進数>2進数と10進数にとって都合の良い基数を使って10進数を経由した計算方法がとれます。
以下の例は、まだ解き方を書いていないので、今分からなくても大丈夫です。
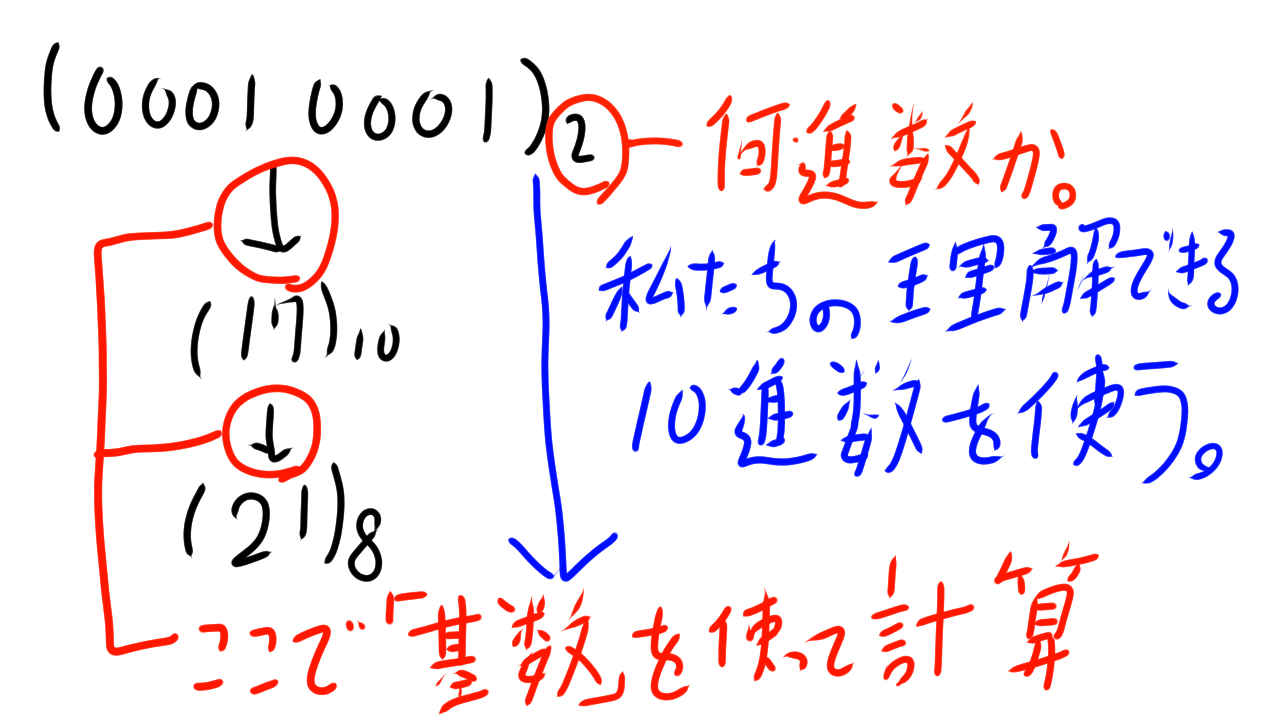
00010001という2進数を8進数に変換すると21になるのですが、この計算の中で基数を使います。
基数をつかって2進数の00010001は、10進数では17だということを求め
基数を使って10進数の17は、8進数では21だということがわかります。
下図黒色の矢印の部分の計算を基数を使ってできるようにします。
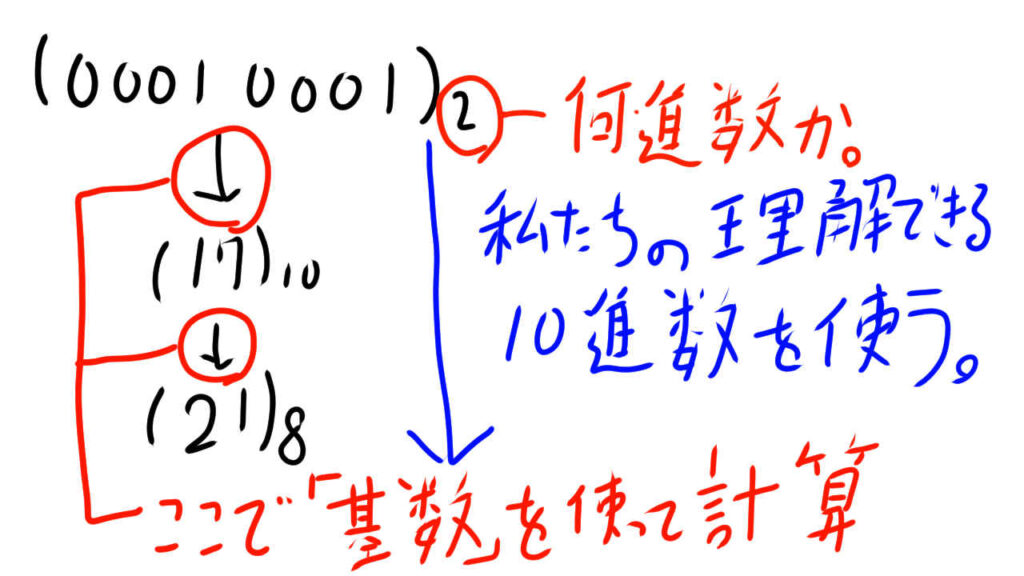
基数を理解する一歩目、基数と10進数、基数と各進数の関係 基本情報技術者試験
私は、基本情報技術者試験テキスト最初の進数変換について、とにかく基数という考え方が全く理解できませんでした。
実際には、計算を色々試してみるのが速いのですが、
少しでも理解するために一番役立った考え方が、先ほどから出ているワード「基数は10進数にとって都合が良いもの」という考え方です。
基数として語られる、2進数の「2」、8進数の「8」、16進数の「16」これらは全て10進数の数字達です。
基数は10進数にとって都合が良いものだからです。
「基数は10進数にとって都合が良いもの」という感覚がかなり大事です。
何も知らず、算数が苦手な私にとっては感覚と文章による理解が重要でした。
基数を文で表現してみる 基本情報技術者試験
基数というものを文章で表現すると
「基数がnの進数をn進数と呼びます。
n進数が1桁で表現できる10進数の最大値はn-1です。 0 ~ n-1
10進数で「n」と呼ばれる数値をn進数で表現する場合は、桁上がりをして"10"になります。」
言い換えると「基数がnの進数は、nで桁上がりする。」です。
です。(次の章から基数を計算に使いますが、まずは感覚と文章に触れます)
とにかく「基数は10進数にとって都合が良いもの」ということを頭の中に置いて文章を見ていきます。
突然でてきた「n」とは、プログラミングでいう変数で、↑の文章のnの部分にはどの10進数の数値を入れても成り立ちます。
他の進数に当てはめてみます。
「基数が2の進数を2進数と呼びます。
2進数が1桁で表現できる10進数の最大値は1です(2-1)。 0 ~ 1
10進数で「2」と呼ばれる数値を2進数で表現する場合は、桁上がりをして"10"になります。」
「基数が8の進数を8進数と呼びます。
8進数が1桁で表現できる10進数の最大値は7です(8-1)。 0 ~ 7
10進数で「8」と呼ばれる数値を8進数で表現する場合は、桁上がりをして"10"になります。」
「基数が16の進数を16進数と呼びます。
16進数が1桁で表現できる10進数の最大値は15です(16-1)。0 ~ F
10進数で「16」と呼ばれる数値を16進数で表現する場合は、桁上がりをして"10"になります。」
なんとなくで文を元に表をつくりましたが、この表は特に考えなくても理解しなくてもいいと思います。
| 10進数 | 2進数 | 8進数 | 16進数 |
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 10 | 2 | 2 |
| 3 | 11 | 3 | 3 |
| 4 | 100 | 4 | 4 |
| 5 | 101 | 5 | 5 |
| 6 | 110 | 6 | 6 |
| 7 | 111 | 7 | 7 |
| 8 | 1000 | 10 | 8 |
| 9 | 1001 | 11 | 9 |
| 10 | 1010 | 12 | A |
| 11 | 1011 | 13 | B |
| 12 | 1100 | 14 | C |
| 13 | 1101 | 15 | D |
| 14 | 1110 | 16 | E |
| 15 | 1111 | 17 | F |
| 16 | 10000 | 21 | 10 |
これが「基数」と「10進数」そして「各進数」との関係です。
ここまでで私が一番大事だと思う感覚は「基数は10進数にとって都合が良いもの」です。
今感覚の上で考えてないとき、私は訳がわかりませんでした。
とにかく人間が一番慣れ親しんでいる10進数を基準に考える方法をお勉強している、という感覚です。
基数と一緒にでてくる「重み」について理解する 基本情報技術者試験
「n進数の基数はnであり、n進数のx桁目の重みはnx-1である。」
計算の直前にも一個、進数変換に大事な「重み」の概念に触れます。
重みの理解には、算数?数学?の「べき乗」の理解が必要です。
べき乗は数字の右上に小さい数字が書いてあるやつです。例)23
私独自の、べき乗に対する理解の仕方としては、「まず、1が存在する。nxとは、1にnをx回掛け算していく。」ということとして理解しています。
まず、1が存在するので、べき乗が0のときは1です。
nxの式としては1のあとに べき乗の数(右上の数字)だけ * n が繋がっていくイメージです。
重み、、、これもとにかく、10進数にとって都合が良いものです。
「n進数の基数はnであり、n進数のx桁目の重みはnx-1である。」です
例えば"2進数の4桁目"は、nを2、xを4として「n進数のx桁目の重みは、nx-1」に当てはめて考えてみると
23となります。
2の3じょうを示す「べき乗」であり「1に2を3回掛け算する」ことを示します。
1 *2 * 2 * 2 という計算になります。 1 * 2 * 2 = 4で、さらに4 * 2で 答えは8になります。
右上の数字が0の時(重みで言う1桁目の時)は、どの数字でも 例えば160の時は1になります。
(なぜ0なのかを知ろうとすると数学の計算式をいっぱい理解しないとダメみたいです。とにかく便利なものとして、0乗のときは1と覚えましょう。つまり、何進数だとしても1桁目の重みはn1-1 つまり0乗となり、絶対1になります。)
私独自の、べき乗に対する理解の仕方としては、「まず、1が存在する。nxとは、1にnをx回掛け算していく。」ということとして理解しています。
まず、1が存在するので、べき乗が0のときは1です。
重みについて2進数を例にみてみます。
2進数の格桁、一桁ずつに入っている数字を10進数に変換するときに使えるのが、重みです。
1桁目の重みは 20(2の0乗)となり、1になります。(1)
2桁目の重みは 21(2の1乗)となり、2になります。(1 * 2)
3桁目の重みは 22(2の2乗)となり、4になります。 (1 * 2 * 2)
4桁目の重みは 20(2の3乗)となり、8になります。(1 * 2 * 2 * 2)

では、16進数の2桁目はどうなるでしょうか。
162-1 = 161 = 1 * 16 = 16 です。
16進数の4桁目の重みは
164-1 = 163 = 1 * 16 * 16 * 16 = 4096 です。
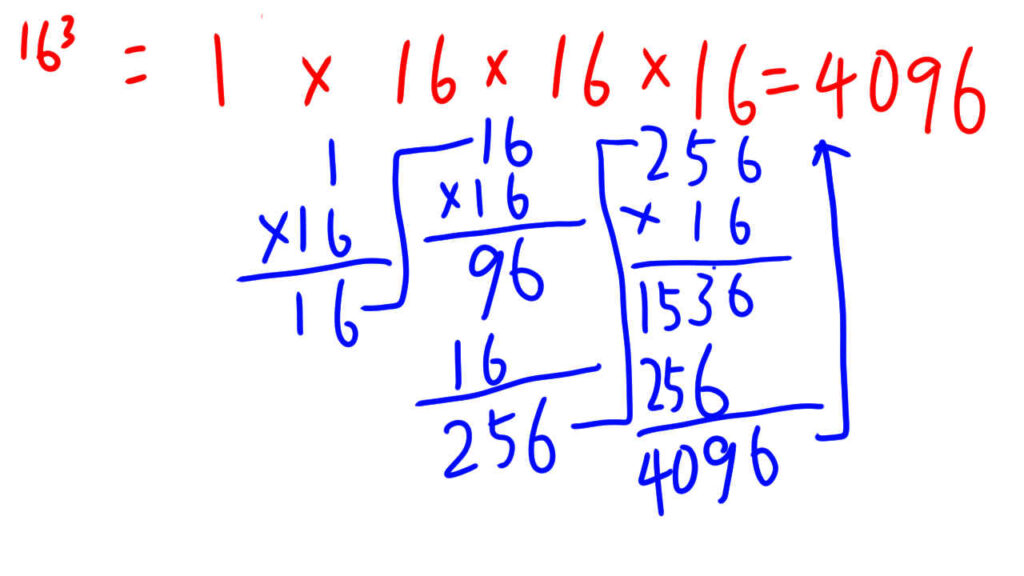
これが、n進数のx桁目の重みを計算する方法です。
「n進数の基数はnであり、n進数のx桁目の重みはnx-1である。」
基本情報の進数変換で、別進数から10進数へ変換してみる
「n進数から10進数に変化するときは、変換前の各桁の数値に重み(nx-1)をかけていき、足し算する。」
あくまで私たちの生きる10進数の世界からの視点であることを忘れないでください。
2進数で1なら、10進数で認知すると1
8進数で6なら、10進数で認知すると6
16進数でBなら、10進数で12
(0001 0101)2 を10進数に変換してみましょう。
(0001 0101)2 の右下の小さな 2 は、何進数の数値かを示すもので、今回は2進数であることを示しています。
まずは、各桁の重みを求めます。実際には数をこなすうちに各進数の各桁の重みは覚えてしまうようです。
「n進数から10進数に変化するときは、変換前の各桁の数値に重み(nx-1)をかけていき、足し算する。」
ということなので、(0001 0101)2 の場合、0ではない桁の重みをまずはもとめていきましょう。

かけざんの中身
「n進数から10進数に変化するときは、変換前の各桁の数値に重み(nx-1)をかけていき、足し算する。」
に従うと、次に各桁にある数字を重みに掛け算して足していきます。
0には何を掛け算しても0なので、数値が0の桁は無視しました。
ここまでくれば、今回は2進数なので計算が単純です。
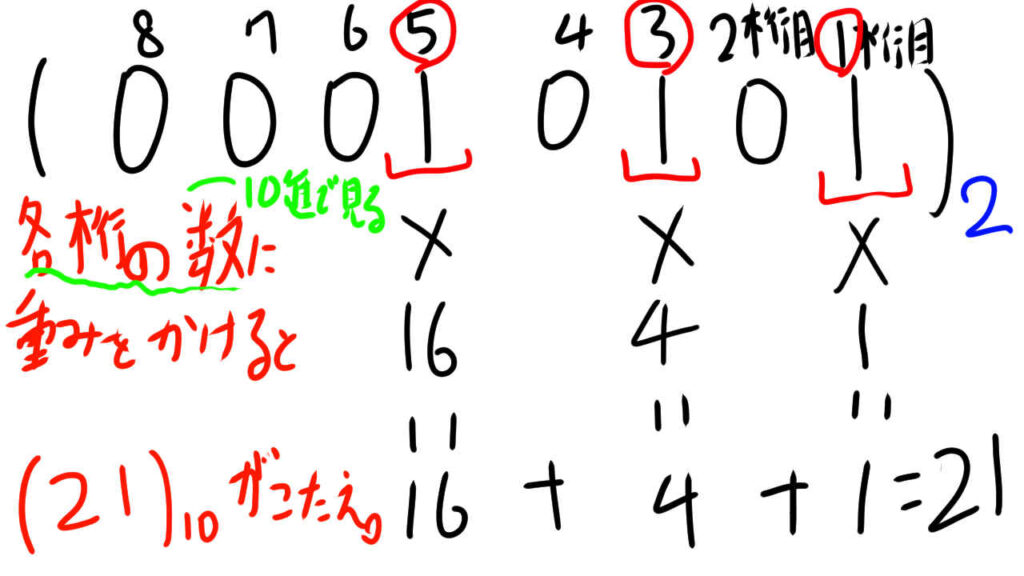
(0001 0101)2 を10進数に変換すると(21)10 になります。
他の進数例えば16進数から10進数に変換するときも同じ
16進数から10進数も同じ方法で変換できます。
(FA5)16を10進数に変換してみます。
各桁の数値を10進数で解釈した数に、重みをかけざんして足します。
まずは、各数値の桁の重みを求めます。
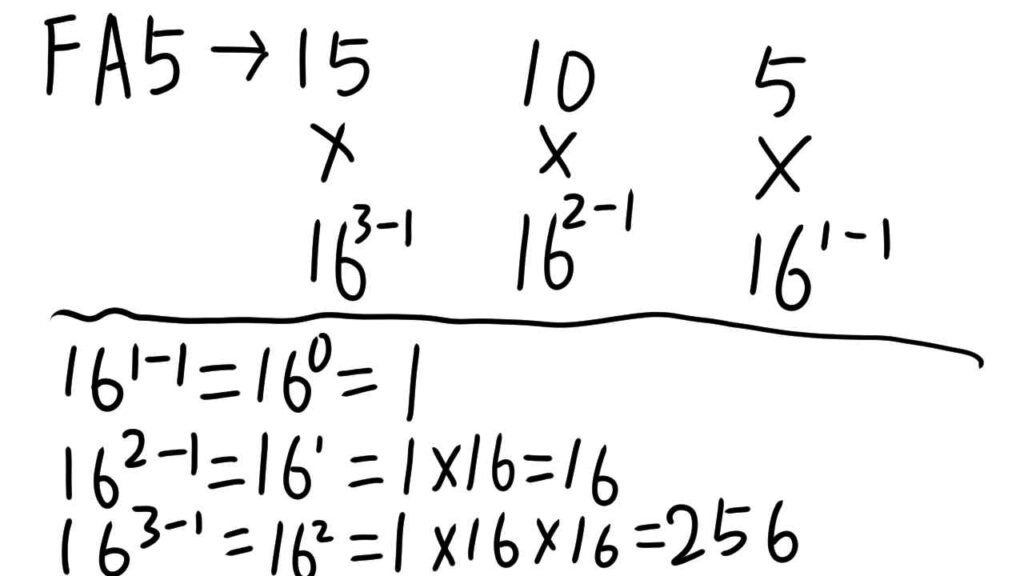
各桁の重みが、1、16,256とわかりました。
各桁の数値を10進数で解釈した数と重みをかけ算して足します。
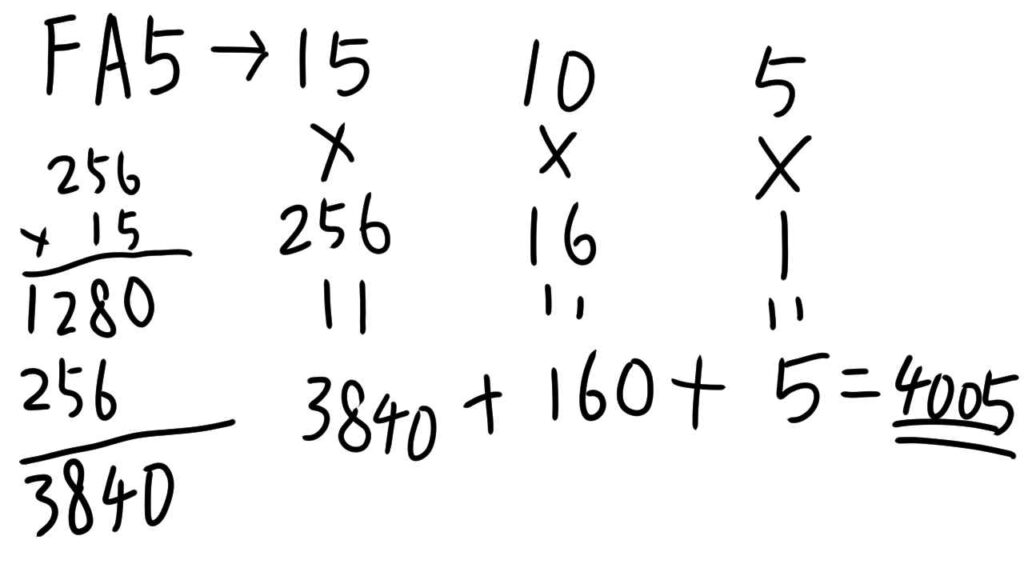
(FA5)16を10進数に変換すると(4005)10となりました。
基本情報の進数変換で、10進数から別進数へ変換してみる
「10進数からn進数へ変換する場合、10進数の数をnで割り、その「あまり」を取り出す。割った答えが0になったら、取り出した余りを逆順に並べる。それぞれの余りを変換先の進数で表記する。」
実際に
(178)10を2進数にすると(10110010)2になります。
1割る2のように、「割りたい数」より「何で割るかの数」のが大きいときは
答えは 0...あまりが「割りたい数」 つまり 1割る2の時は
0あまり1 となることを覚えておく必要があります。

試しに戻してみると、ちゃんと178になります。

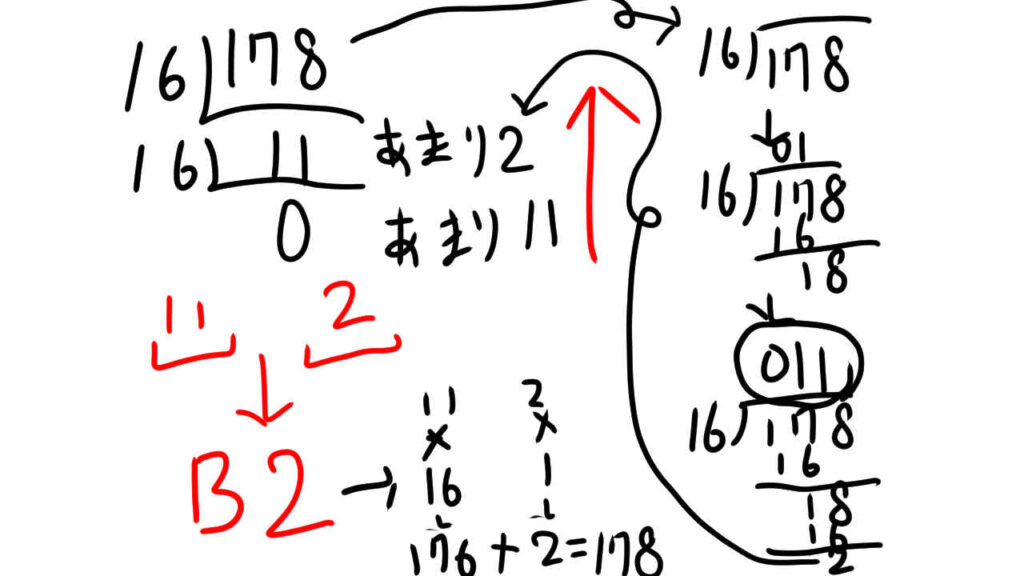
10進数から16進数へ変換してみる
先ほどと同じ考え方で、(178)10を16進数に変えてみると、(B2)16となります。
一旦ここまで
今回は、私が基本情報技術者試験で進数問題に取り掛かった際に、一番最初に壁だった
「基数」「重み」「進数変換」に関するメモでした。
私が使用している教科書は⇩です。
少数部分の10進数から2進数への変換
(13.15)10を2進数に変えてみると、(1101.001001...)2となります。
13.15の13の部分はこれまでの通り、13 mod 2 ⇨ 6 mod 2 ⇨ 3 mod 2 ⇨ 1 mod 2 の答えを逆から←並べて、1101となります。 mod といのは x mod y の場合、xを7で割って余った数 です。
次に0.15の部分の求めかたは、小数分に基数をかけて小数点より左側の整数部分を取り出して並べていきます。
小数部分が0になったら終わりで、無限小数となる場合もあります。
⇩
0.15 * 2 = 0.3 ... 0
少数部分に基数をかけて、整数部分の数を取り出します。 0
0.3 * 2 = 0.6 ... 0
同じく少数部分に基数をかけて、整数部分の数を取り出します。 0
0.6 * 2 = 1.2 ... 1
同じく少数部分に基数をかけて、整数部分の数を取り出します。 1
0.2 * 2 = 0.4 ... 0
同じく少数部分に基数をかけて、整数部分の数を取り出します。 0
0.4 * 2 = 0.8 ... 0
0.8 * 2 = 1.6 ... 1
0.6 * 2 = 1.2 ... 1
今回の場合は無限小数となり、ループする形なので打ち切って(1101.001001...)2となりました。
無限小数の扱いなどは本番では問題文や選択肢でわかると思います。
10進数の少数を16進数にする場合も考え方は同じ
(234.67)10 の整数部分を計算
234 / 16 = 14 ... A
15 / 16. = 0 ... E
↑
EA.
次に小数部分を計算
⇩
0.67 * 16 = 10.72 ... 10 = A
0.72 * 16 = 11.52 ... 11 = B
0.52 * 16 = 8.32 ... 8
0.32 * 16 = 5.12 ... 5
0.12 * 16 = 1.92 ... 1
0.92 * 16 = 14.72 ... 14 = E
よって無限小数が確定
EA.AB851E...
となります。







コメント